728x90
곱법칙
함수(구함수) f와 g가 모두 미분 가능일 때, 함수들을 곱하거나 나누어 얻어지는 새로운 함수의 도함수 역시 구할 수 있다.
먼저, 곱법칙(product rule)은 두 구함수를 곱하여 얻은 새로운 함수의 도함수를 구하는 방법이다.
곱법칙

- 두 함수의 곱의 도함수는 앞의 함수에 뒤의 함수의 도함수를 곱한 값에, 뒤의 함수에 앞의 함수의 도함수를 곱한 값 둘을 더한 것과 같다.
몫법칙
한편, 몫법칙(quotient rule)은 두 함수를 나누어 얻은 새로운 함수의 도함수를 구하는 방법이다.
몫법칙
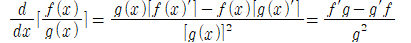
연쇄법칙
연쇄법칙은 합성함수(composition of two functions)를 미분하는 방법이다.
만

와 같은 함수를 미분할 경우, 지금까지 배운 미분 공식으로는 이를 풀 수 없을 것이다.
이때, y=f(u)=5√u, u=g(x)=x³+1로 두면, y=F(x)=f(u)=f(g(x))로 고쳐 쓸 수 있다.
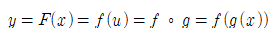
연쇄법칙(chain rule)
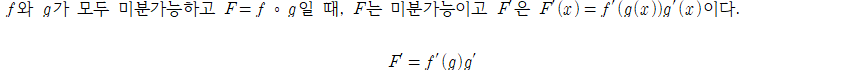
라이프니츠 기호로 chain rule을 쓰면 다음과 같다:
dy/dx = (dy/du)(du/dx)
-y는 u의 함수이고, u는 x의 함수이다.
-연쇄법칙은 다음과 같은 풀이 전략을 갖는다.
[1] 합성함수가 h(x) = f(g(x)) 꼴 일 경우, f(x)와 g(x)를 먼저 규명(identifying)한다.
[2] f'(x)를 구한다.
[3] f'(g(x))를 구한다.
[4] g'(x)를 구한다.
[5] h'(x)은 f'(g(x))g'(x)이다.
728x90
'knowledge > math' 카테고리의 다른 글
| [ 미분 ] 9. 도함수 : 지수함수와 로그함수의 도함수 (0) | 2022.12.24 |
|---|---|
| [ 미분 ] 8. 도함수 : 삼각함수의 도함수 (0) | 2022.12.23 |
| [ 미분 ] 6. 도함수 : 다항함수의 도함수 (1) | 2022.12.19 |
| [ 미분 ] 5. 도함수 : 입문 (0) | 2022.12.18 |
| [ 미분 ] 4. 점에서의 변화율 (0) | 2022.12.16 |
![[ 미분 ] 7. 도함수 : 곱법칙과 몫법칙, 그리고 연쇄법칙](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcJPy7V%2FbtrUattVtmd%2FZlttPmCXfdCz4sHyK39Mr1%2Fimg.png)