삼각함수란 각도와 관련된 여러가지 함수로 sine 함수, cosine 함수, tangent 함수가 있으며 이들의 역수 cosecant, secant cotangent를 모두 합쳐 총 6개이다.
삼각함수의 정의

삼각함수는 먼저 직각 삼각형을 통해 다음과 같이 정의할 수 있다.

삼각함수의 직각삼각형 정의의 역수는 각각 코시컨트, 시컨트, 그리고 코탄젠트의 정의와 같다.
또한 단위원(unit circlr:반지름 r이 1인 원으로 원점 (0,0)을 중심으로 한다.)으로 삼각함수를 정의할 수도 있다.

반지름을 r이라 둘 때, 각 삼각함수의 정의는 다음과 같이 정리한다.
- sinθ = y / r
- cosθ = x / r
- tanθ = y/x = sinθ/cosθ
- secθ = 1/cosθ
- cscθ = 1/sinθ
- cotθ = 1/tanθ = cosθ/sinθ
sine 그래프와 cosine 그래프, tangent 그래프는 아래와 같이 그릴 수 있다

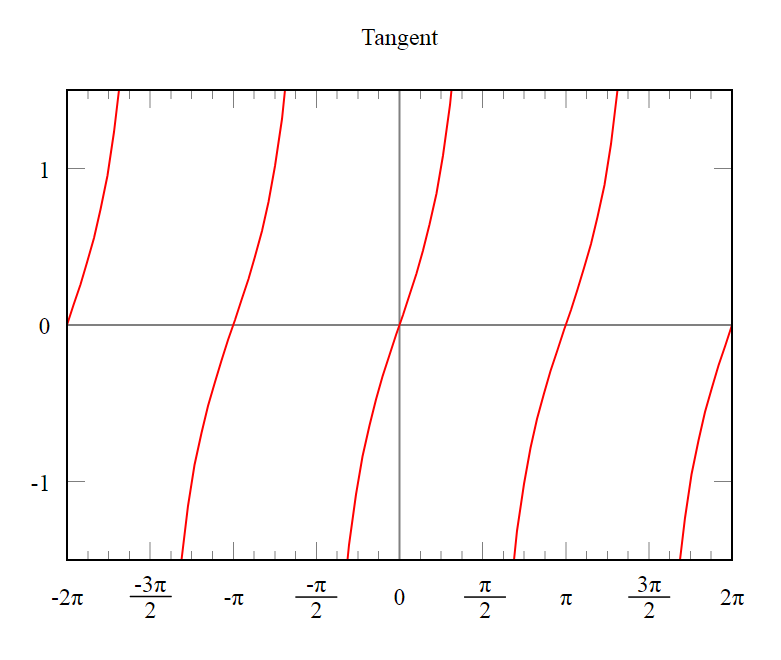
삼각함수의 성질
삼각함수는 다양한 정의만큼 여러가지 성질을 가지고 있는데, 자주 사용하는 삼각함수의 성질을 다음과 같이 정리할 수 있다.
1.주기성 : 삼각함수의 그래프를 통해 이들이 2π(sine, cosine) 혹은 π(tangent)의 주기(period)를 가짐을 알 수 있다.
2. 특수각에서의 삼각함수의 값

3. 항등식 : 삼각함수가 나오는 항등식으로 복잡한 삼각함수 식을 간단히 정리하는데 유용하다.
-특히 적분 파트의 삼각치환적분에서 매우 자주 쓰인다.
(1) 피타고라스 정리

여기서 sin²(x)는 (sinx)² 와 같다.

(2) 삼각함수의 덧셈정리
두 삼각함수를 연결하는 연산자의 종류에 따라 2가지 항등식을 가지며, 이들은 삼각함수의 가법으로 쉽게 유도할 수 있다.
삼각함수의 가법

삼각함수의 합곱 변환식

삼각함수의 곱합 변환식

(3) 삼각함수의 배각공식
삼각함수의 가법으로 배각공식을 유도할 수 있다.
배각공식

(4) 사인법칙과 코사인법칙

삼각함수의 도함수
삼각함수의 도함수에 들어가기에 앞서 삼각함수의 극한 값으로 두 가지 식을 확인하자.

도함수의 기본 정의를 통해 삼각함수와 역삼각함수의 도함수는 아래의 도표와 같이 정리할 수 있다.

'knowledge > math' 카테고리의 다른 글
| [ 미분 ] 10. 음함수 미분법(Implicit Differentiation) (0) | 2022.12.25 |
|---|---|
| [ 미분 ] 9. 도함수 : 지수함수와 로그함수의 도함수 (0) | 2022.12.24 |
| [ 미분 ] 7. 도함수 : 곱법칙과 몫법칙, 그리고 연쇄법칙 (0) | 2022.12.20 |
| [ 미분 ] 6. 도함수 : 다항함수의 도함수 (1) | 2022.12.19 |
| [ 미분 ] 5. 도함수 : 입문 (0) | 2022.12.18 |
![[ 미분 ] 8. 도함수 : 삼각함수의 도함수](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbN5mIS%2FbtrUlBfAiKg%2Fx5gIQCUmzP2ppToKKn7pik%2Fimg.png)